
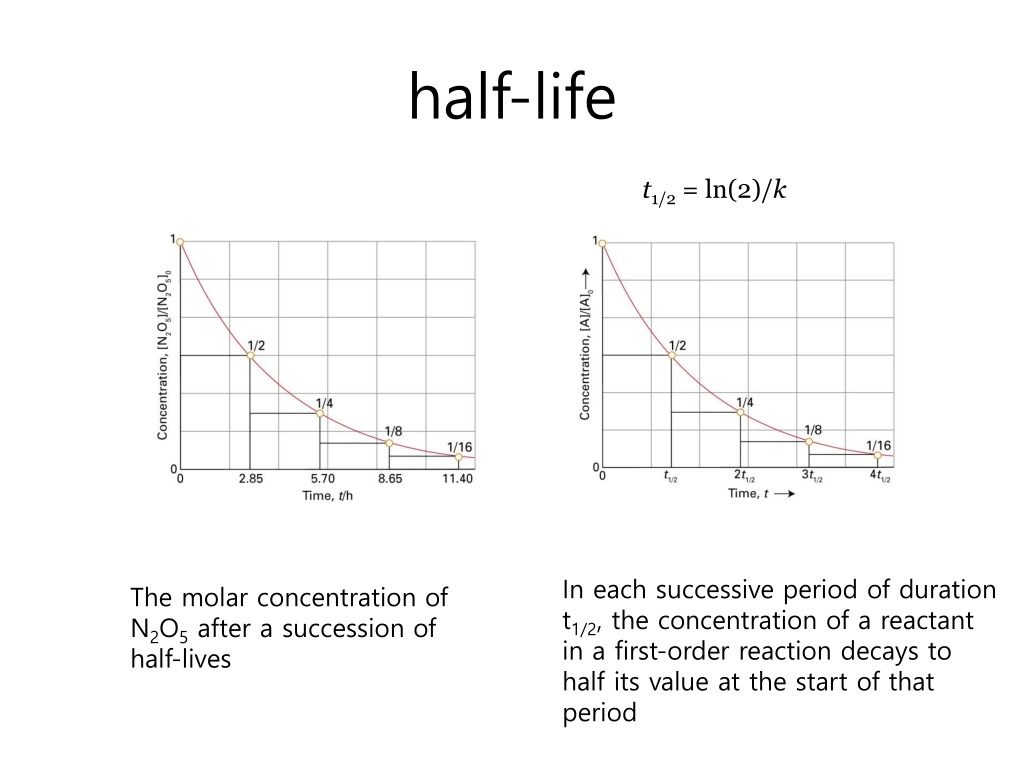
Most calculators probably want you to enter the number 2 and then press the ln button. Somewhere on your calculator is a button marked "ln". If you have no idea what that means, it doesn't matter in the least. This only applies to first order reactions. For first order reactions there is a simple relationship between this and the rate constant for the reaction, k. The relationship between half-life and rate constant for a first order reaction Only first order reactions have a constant half-life. This isn't a problem you need to worry about for CIE purposes.Īll you need to recognise is that the concentration against time curve for:Ī zero order reaction will be a straight line Ī first order reaction will be a curve with a constant half-life.Īny other order of reaction will be a curve with a non-constant half-life. If you did this for a reaction with some other order (second order, for example, or some fractional order), then the values won't be constant. you can see that the time taken to halve the concentration is always the same. Or you could measure it from the original 100% to 50%, and then compare that with the fall from 80% to 40%, and from 60% to 30% - or any other combination of concentrations, as long as you are measuring the time taken to halve the concentration. You simply have to measure how long it takes for the concentration to fall from its original value to half of that value then measure it from a half to a quarter then from a quarter to an eighth. You can easily discover this from a graph of concentration against time. It doesn't matter what concentration you start with, it will take exactly the same time for the concentration to reach half of that value. The half-life of a reaction is the time it takes for the concentration of a substance to fall to half of its original value.įor a first order reaction (but only for a first order reaction), the half-life is constant.


And this is where the concept of half-life comes in. It starts more steeply, but you need to investigate the curves more carefully to be sure. A second order curve isn't hugely different. A typical first order curve will look like this:īut you can't tell it is first order just by looking at it. It will start to curve at that point.Ĭoncentration-time graphs for a first order reactionįirst order reactions will have a curve if you plot concentration against time (but so will other orders as well - apart from zero order). Eventually the concentration will get low enough that the special circumstances which caused the reaction to be zero order won't apply any more. If you draw a graph like this for a zero order reaction, be careful not to extend it too far. If the rate doesn't change, that means that the slope of the curve doesn't change - and so you will get a straight line rather than a curve. In this case, the rate of reaction won't change as the concentration of the substance falls over time. So what happens if the rate is independent of concentration, as in a zero order reaction? That is because the concentration is falling, and rate is normally dependent on concentration. The curve starts off falling steeply, but then gets gradually less steep. Normally, when you plot a graph of concentration of a substance against time, it looks something like this: Increasing the concentration of A can't make any difference, because the catalyst is already working as fast as it can. This can happen, for example, where the reaction is taking place on the surface of a catalyst, where the concentration of A is high, and all the active sites on the catalyst are already fully used by the reactant. Under some rather special circumstances, the rate of reaction may not be affected by the concentration of the reagent. What follows is a brief summary.Ĭoncentration-time graphs for zero and first order reactionsĬoncentration-time graphs for a zero order reactionĪssume that you have a reaction which involves a single reagent A. Quite a lot of this is covered in detail in my chemistry calculations book. I have also included statement 8(g) (ii) on this page because it is closely related.īefore you go on, you should find and read the statements in your copy of the syllabus. This statement is about concentration against time graphs in rate of reaction work, and their relationship with the half-life of a reaction. Chemguide: CIE A level chemistry support: Learning outcome 8(h)Ĭhemguide: Support for CIE A level Chemistry


 0 kommentar(er)
0 kommentar(er)
